Examples of maths magic found in nature
When people talk about the magic in maths, which unfortunately only happens on rare occasions, we quickly think we need to know very advanced maths to see and experience that. However, the beauty of maths shows in many magical ways in nature that we can all experience and admire. Understanding the mathematical formulas behind the magic might need more deep background knowledge but experiencing the magic of maths does not.
Every time you pass a tree on a walk or see a spider web in your basement, you see examples of the wonders of nature, all based on maths concepts. So, maths is all around us, and sometimes we just need a reminder to see it more precise. If you begin to acknowledge the maths in nature today, you will see its beauty everywhere every day. Once you have seen it, you can’t unsee it!
Today, we want to share examples of maths concepts that magically just exists in nature. These are examples of the beauty of maths that we often miss, but we can learn to start seeing again. So why not go on a maths walk with your child and search for maths in nature together?


One common way in which you can see maths in nature is through symmetry! Our surroundings are filled to the brim with so many beautiful and precise symmetrical patterns that it is almost unbelievable.
Symmetry can take many different forms. One of them is bilateral symmetry, in which an object has two sides that are mirror images of each other. Some examples of where in nature you can see this is in butterflies, leaves, and faces of both animals and humans. The human body is also a great and accessible example of a living being that has bilateral symmetry!

Bilateral symmetry can be seen on the wings of a butterfly where both the right and the left sides are exact copies of each other.
Another form of symmetry that we can find in nature is radial symmetry, which has a fixed point, known as the centre, where the symmetry begins. From the centre point, you could draw numerous lines of symmetry. Some examples of radial symmetry in nature are flowers, spiderwebs, and snowflakes.

The flower pattern follows a radial symmetry. The petals are equally spread out from the circle in symmetry.
Snowflakes are also actually extra magical. Not only are they completely symmetrical, but no individual snowflake is alike another. Imagine how many snowflakes it takes to cover a field or a house roof with snow, then think about the fact that every snowflake is unique. How can nature create that by itself? That is a remarkable example of math magic in nature!

Each snowflake in a field of snow is perfectly symmetrical but also has its unique shape. Incredible, isn’t it?
Another example of radial symmetry in nature is spider webs. Even though not all of us fancy spiders at all, we can’t help to be mesmerised by their symmetrical ways of wowing their webs. Not all spiders spin webs in this way, but those who do are called orb-web spiders. They create almost perfect circular webs with equal distanced radial supports coming out of the middle of the web, creating a spiral to catch prey. No one knows why orb spiders are so geometrically inclined. Neither are these webs better at catching prey than irregularly shaped webs. However, some scientists theorise those spiders build orb webs for strength. The radial symmetry distributes the force of impact when a spider’s prey gets stuck in the web – which would mean there’d be less of a risk of rips in the thread.

Why orb-web spiders are wowing their webs in perfect symmetry is still a mystery to us. But neither less, it is an example of how maths shows in nature.
Either way, it is fascinating to think that even so small creatures as spiders are working with geometrical forms and symmetry. Symmetry just happens to appear everywhere in nature. We just need to look closely to see it.
Fractals
A fractal is a never-ending and self-referential pattern that repeats itself at different scales. It might sound like a complicated process and rare occurrence, but the truth is that fractals are everywhere in nature! Even though the patterns themselves are complex, they show up in the most unlikely places in nature. Examples of where you can see fractals in nature are trees, lightning, and even our human bodies as, for example, blood vessels!

Even lightning, one of the most forceful occurrences in nature, is an example of fractions shown in nature.
Trees and their ecosystem might be one of the most accessible ways to experience and explore fractals in nature. There you can find fractals in the entire life cycle of a tree, all the way from the patterns of a seed and the tree’s branches to the leaves and pinecones. For example, if you look closely at a leaf, you can see its veins that form an irregular and recurrent pattern – fractals! Another clear example of fractals in leaves is the fern. The fern is built on the exact shape that repeatedly repeats itself in smaller and smaller scales.

If you look closely at a leaf, you will see fractions after fractions. The structure of a leaf mirrors the exact shape of fractions that a tree has.

A fern is based on the same basic shape, repeated repeatedly in smaller and smaller shapes. If you look closely, each tiny fern leaf is a copy of the whole fern leaf itself.
Going back to the trees, as a tree’s trunk grows, it produces a branch with two growth points. One of the new stems will branch into two, while the other stays idle. This branching pattern repeats for each of the new stems and keeps repeating as the tree grow. Therefore, a tree is not only a tree but also a perfect mathematical example of nature’s fractals!

Every branch of a tree breaks up similarly to the previous branch. Each tree branch is a smaller tree shape, making trees an excellent example of fractals in nature.
Another magical aspect mathematical fractal growth pattern of a tree is how the branches relate to the total thickness of the trunk. Trees grow so that the entire thickness of their branches at a particular height equals the thickness of their trunks. This occurrence was first noticed by no other than Leonardo Da Vinci. It has since then been hypothesised and observed by botanists to find an answer to why this is. Some thought the tree produced this pattern connected to how it pumps water from its roots to its leaves.

A scanned image of Leonardo Da Vinci’s notebook, theorising the thickness of a tree trunk in relation to the thickness of the branches of the tree at a particular height.
However, it was not until 2011 when a specialist in fluid mechanisms used mathematics to find out that the trees fractal pattern instead has to do with the wind distribution. The pattern prohibits branches from breaking from the wind in the same way that manufactured structures have been designed to do the same. So, in that sense, trees knew about how to handle wind long before we did – through a perfect mathematical calculation. Magical isn’t it!
Pi
Pi is truly magical; it is an infinitive number (!) that appears everywhere in the universe. Yet, even though we know a lot about Pi today, we still know nothing. Mathematicians have been trying to find the value of Pi for over 4000 years, a search that’s still happening.
Earlier this year, a supercomputer calculated Pi to 62.8 trillion digits, breaking the earlier record of 50 trillion calculated digits. That’s a number so huge that it would take 664.128 years to count all those digits out loud. But for most of us, we know Pi as 3.14 and the ratio of a circle’s circumference to its diameter, something we learn in elementary geometry in school.
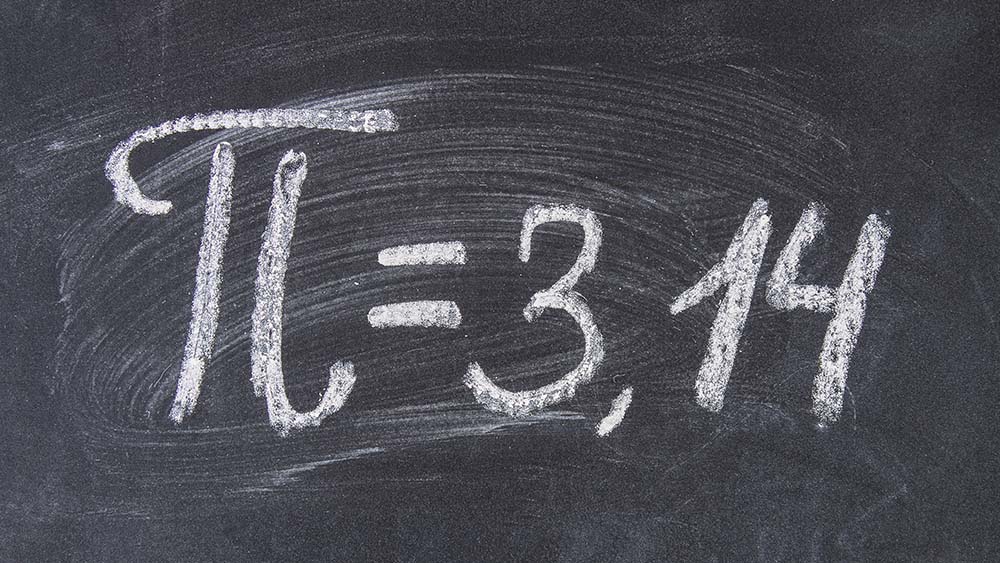
The majority of us knows Pi as 3.14 – But the truth is that Pi has an infinite number of digits. As of today, we know 62.8 trillion of its digits.
Believe it or not, but Pi appears everywhere in the universe, even in places and situations where it doesn’t seem to have a connection to a circle. You can find it in physics, engineering, and of course, in maths. Pi just happens to appear everywhere in the universe, for example, in electromagnetic waves, the structure of DNA, and the colours of auroras. You can also find Pi in the orbits of planets. So if we wanted to describe the structure of the universe or find the relationship between planets, Pi is what we would have to use.

You can find Pi everywhere! One example is in the structure of our DNA.
But there are also more accessible examples of where you can find Pi without having to travel to space or look at a string of DNA. For example, anything that involves a circle or a sphere is about Pi, and both spheres and circles appear everywhere in nature. So one easy way of seeing Pi in nature is to look out for circles and spheres, such as bubbles, raindrops, and tree rings. If you start looking for Pi by finding circular objects in nature, you will soon realise that they are everywhere.
Maths magic is all around us
As you see, math is genuinely all around us. To summarise, you can find the language of mathematics inscribed in everything. You can find it in unbelievable huge things like the universe or tiny places like in the details of a leaf or a snowflake.
For many of us, the mathematics behind these structures might still be ungraspable. To experience many of the beautiful parts of maths, we need a lot of background knowledge.
But just the realisation that maths is the building block of almost everything can make us appreciate maths in a new way. And we don’t need the maths knowledge to enjoy the beauty maths creates, like the symmetry of a snowflake or the fractal branching of a tree.
Since maths is in so many of the universe’s and world’s secrets, it also gives us more reasons to learn maths. These secrets can only be revealed and understood through mathematics. And it is worth it! If you can see and enjoy this beauty without knowing maths, imagine the beauty you could see if you had a better understanding of the mathematics behind it.


